- Présentation
Un des mondes particuliers est le Monde Symétrique. Ce monde est formé par la répétition à l'infini d'un même motif, le motif Monde Symétrique. Une personne est simultanément dans tous les motifs. Les axes (plans) de symétrie passent par le lac et le gros pilier noir (hauteur infinie). En ces deux points, on a donc une symétrie centrale : un personnage qui arrive au pilier ou à l'île du milieu du Lac y arrive de deux côtés opposés simultanément. Ce monde est parfois utilisé par les magiciens pour tester les nouveaux adeptes ou alliers. L'idée m'est venue au Lycée après avoir lu une BD de la série « Les Aventures d'Anselme Lanturlu », tome « Le Géométricon » de Jean-Pierre Petit aux éditions Belin. Ce livre pourra vous donner beaucoup d'idées de mondes originaux.
- Arrivée, l'énigme pour sortir

L'arrivée se fait sur le haut plateau. Sur sol, est gravé en Celte, les inscriptions si contre. Les différences typographiques entre les mêmes lettres sont là pour aider la résolution. Devant les gravures, on trouve un pousse-pousse avec les lettres suivantes dans le désordre. Il est gravé dans la pierre.

Si on ordonne le pousse-pousse en suivant les indications, on doit trouver :
Au centre de l'île du Lac, il y a une tour. Pour en sortir, chaque personnage s'y trouvant doit se serrer la main dans cette tour : il arrive face à lui (symétrie centrale) et peut se serrer la main. Attention, l'image n'est pas comme celle renvoyée par un miroir (symétrie par rapport au plan du miroir) : si nous bougeons notre main droite, c'est la gauche du miroir qui bouge. Mais au centre de l'île, si l'aventurier bouge sa main droite, son image (lui-même) bouge aussi la main droite. Ceci peut-être déconcertant pour quelqu'un qui adore se regarder dans un miroir.
- Similitude directe ou indirecte
- Présentation
Lorsque vous êtes devant un miroir, l'image que vous voyez de vous n'est pas celle que vos interlocuteurs voient : la droite et la gauche sont inversées. Entre votre image et vous il y a une similitude indirecte. Cette symétrie est la même que celle entre vos deux mains : elles sont presque semblables, mais inversées, il y a une différence entre une main gauche et une main droite (côté du pouce par exemple).
L'autre similitude se trouve par exemple quand, à partir d'un même moule, on fait des figurines : elles sont toutes identiques (aux défauts de fabrication prêts). Pour passer d'une figurine à l'autre, il y a une similitude directe.
Si nous regardons notre image à travers deux miroirs, on aura bien notre gauche à gauche et notre droite à droite : Chaque miroir représentant une similitude indirecte, le passage de deux miroirs donnera une similitude directe. 3 miroirs inverseront la gauche et la droite : similitude indirecte. Par extension, si on passe un nombre pair de miroir (ou plan de symétrie dans mon monde), on conserve notre gauche à gauche et la droite à droite (similitude directe). Si par contre le nombre de miroir est impair, la gauche et la droite sont inversées (similitude indirecte).





- Similitude indirecte
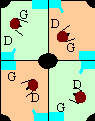
Notre monde symétrique est la juxtaposition, comme indiqué ci-dessus d'un même motif. Pour passer d'un motif à son voisin (fond vert à fond beige ou vise versa), il suffit de faire une symétrie verticale pour un déplacement horizontal (droite-gauche ou gauche-droite) ou une symétrie verticale pour un déplacement vertical (haut-bas ou bas-haut).
J'ai représenté un bonhomme dans mon premier plan (fond vert) qui regarde entre ses bras par-devant (comme son nez) et je lui ai fait subir les mêmes transformations que le motif de mon monde. On voit que sa gauche qui est vers le bout du lac bien triangulaire a changé de côté quand on est passé sur le fond beige.
- Similitude directe
Si on regarde les motifs de même couleur, on voit qu'il y en a deux groupes : ceux où le bonhomme regarde à gauche et ceux où il regarde à droite. Pour passer d'un motif à un autre du même groupe, il suffit de faire glisser le motif : une translation. Par contre pour changer de groupe, il faut faire tourner le motif d'un demi-tour (rotation de 90°) et une translation.
Pour bien voir si vous avez compris cela, il ne vous reste plus qu'à essayer de dupliquer le motif pour avoir le tour du Lac en complet. Après il ne reste plus que des translations (glissements) à faire pour tous retrouver.
- Conséquences
Nous avons deux intrépides visiteurs dans ce monde. Supposons qu'un des deux décide de ne plus bouger et d'attendre son camarade. Si son camarade va directement à sa rencontre (déplacement horizontal par exemple), il le rencontrera dans le plan voisin de couleur différente. Lors de leur rencontre, chacun aura l'impression que l'autre a inversé sa gauche et sa droite. Si l'un des deux lit les manuscrits de l'autre, il voit que le sens d'écriture a été inversé ! Tant que les personnages restent ensembles, la seule possibilité de s'apercevoir de cette supercherie est l'énigme pour sortir qui elle change de sens chaque fois qu'on passe un "miroir".
- Bilan
Il faut faire attention au nombre de passages d'axe effectué par chaque aventurier : un nombre impair avant de retourner dans le monde réel, signifiera qu'il a inversé sa gauche et sa droite ! Un nombre pair n'aura aucun effet.
S'il notre aventurier ressort inversé, il lui faudra réapprendre à lire et écrire dans le bon sens pour le faire aussi rapidement qu'avant. S'il était droitier, il devient gaucher et vise-versa.
- Présentation
- Les rencontres
Dans ce monde, on rencontre quelques araignées géantes, des abeilles tueuses géantes et les aventuriers morts ici qui sortiront de terre au passage des aventuriers. Le but des morts est de retourner sur le plan d'origine pour aller Aux Champs Elysés, mais ils se défendront en cas d'attaques.
Un monde a été sélectionné pour y mettre tous les hiatus intéressants : arbres qui courent, marmites qui parlent... C'est le monde où les vieux magiciens entropiques vont passer leur retraite. Ils y invitent parfois de jeunes et expérimentés (moins qu'eux !) magiciens pour partager leurs expériences.
Les magiciens qui y vivent sont fondantalement chaotiques car ce monde génère 10 fois plus d'hiatus : 1 sort sur 2 (tirage pair ou impair sur le jet de variation de niveau). Les magiciens non entropiques ont eux 1 chance sur 10 de découvrir les joies du hiatus à chaque lancé de sorts. Ces derniers ont 2% cumulatifs de devenir magiciens entropiques par hiatus.
On raconte même parfois que de grands magiciens entropiques ont emmené sur ce plan certains de leurs rivaux non entropiques quand ces derniers se montraient trop ouvertement contre leur mode de magie avec ses aléas trop risqués. Ces grands magiciens devenaient, contre leur gré, eux aussi des magiciens entropiques ne pouvant revenir à leur ancien amour la magie propre.
Ce monde est constitué d'un plateau de terrain de plusieurs dizaines kilomètres de largeur. Tous les jours les bords changent (nature chaotique du lieu) : ils perdent ou gagnent, suivant les lieux et les jours, au maximum un mètre d'après les experts. On voit les morceaux tomber dans le vide qui l'entoure quand il diminue, ou on le voit se boursoufler quand il grandit. Pour le moment, personne ne peut ni prévoir ni intervenir sur ses modifications.
- Présentation
Ces mondes sont constitués comme des carreaux les uns à côtés des autres, mais ce sont les mêmes motifs qu'on retrouve d'un carreau à l'autre. On peut ne retrouver d'un carreau à l'autre que les particularités géographiques (multitudes de mondes semblables collés les uns au autres) ou c'est le même univers qui se replie sur lui même (une même plante, un même être vivant seront simultanémént sur tous les carreaux et feront toujours la même chose).
Dans le premier cas, c'est comme un dallage infini où on peut exploiter les carreaux les uns après les autres. Dans le second, c'est comme le monde symétrique défini ci-dessus, lorsqu'on sort par un bord du motif (parfois choisi arbitrairement), en fait, on y rentre par un autre (sans se rendre compte de rien).
- La vie sur place
La viabilité ou la possibilité à un univers qui se replie sur lui même d'entretenir de la vie dépend de sa taille : le motif doit être assez grand pour qu'un écosystème puisse s'y développer. Par contre pour qu'un monde soit viable, il suffit de pouvoir y entreposer un être vivant. Le tout est de savoir qu'elle genre de vie on veut y mettre ou on espère y trouver, pour un être humain, il suffit de peu de place (voir le métro aux heures de pointe), mais c'est avec soi même qu'on jouera du coude si c'est un lieu trop exigü.
- Méthodes de construction
- Les frontières
Pour créer un tel monde il faut prévoir un motif avec des limites qui correspondent entre elles (un jeu de géométrie pas toujours simple). Un bête rectangle ou hexagone avec les côtés opposés (de même longueur) correspondants simplement entre eux est un cas simple où on ne perd pas trop le nord : on peut toujours expliquer au joueur se qu'il a sur la gauche ou sur la droite, on peut faire un dessin à l'infini de ce monde.
- Exemple : L'Hexagone tordu
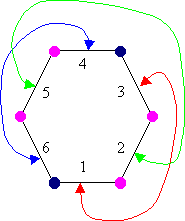
Par contre dans un monde avec de telles correspondances (voir ci contre), il y a de quoi perdre la tête! Mettez vous sur la face 4 au poteau marine qui fait le coin avec la face 3, placez le poteau à votre droite et faîtes en le tour. Vous passez sur la face 6, au coin du 1 (poteau à droite) toujours autour du poteau marine. Continuez, voici la face 1 qui me renvoie à la 3 au coins du poteau marine, si je continue, j'arrive au point de départ : la face 4. J'ai donc fait le tour du poteau marine en 2x120=240°!
Je peux essayer de faire la même chose avec le poteau rose. Je pars la face 5, au coin avec la 4, poteau sur la droite, je passe à la 2 au coin avec la 3, face qui me fait passer à la 1 au coin avec 2, face qui me fait passer à la 5 au coin de la 6, face qui me fait passer au 4, coin avec le 5 : mon point de départ. Cette fois, mon tour s'est fait en 4x120=480°!
Ceci est un problème! Les coins de mon hexagone forment donc des points de ruptures de l'espace! C'est pour celà que j'y ai mis des poteaux (hauteur infinie). Vous pouvez essayer un tel monde, mais dans ce cas, où placer les points cardinaux ? Que signifie aller droit ?
En prenant les poteaux sur la gauche, je fais les mêmes parcours, mais dans l'autre sens. Dans ce monde (ouf!), quand on revient sur nos pas, on revient au point de départ! Cette caractéristique est recommandée car les frontières ne sont donc pas visibles. Dans un monde qui ne permet pas le retour sur ses pas, il y aurait des frontières visibles de non retour : quand on les passe, on ne voit plus ce qui nous entourait avant (comme la queue du cheval qui reste invisible tant qu'il n'a pas fini de passer cette frontière). Ces frontières, on pourrait, par exemple, les représenter comme des miroirs ou des murs opaques ondoyants.
- Les bandes
On peut se proposer de faire des mondes linéaires : une bande infinie avec les bords qui se rejoignent. La jointure peut se faire de différentes manières :
- juste en face : pour revenir sur nos pas, il suffit de marcher perpendiculairement à la direction principale (cf schéma ci contre). Un personnage est dans toutes les bandes en même temps car en faite il n'y en a qu'une, la représentation avec plusieures bandes justaposée est juste pour mieux comprendre la passage d'une frontière (virtuelle).
- en face avec un décalage : dans ce cas, en placant assez de bandes les unes à côté des autres, on comprend que la direction principale a mal été choisie (comme entre les trais rouge du dessin à côté) et qu'il la faire tourner pour revenir au premier cas.






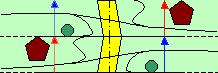
- en face mais avec une symétrie autour d'un point central (comme pour le cas en face, le centre de l'autre côté ,est obligatoirement en face), dans ce cas, à chaque passage, on inverse la gauche et la droite : le centre pase de gauche à droite. Cette inversion est non perceptible par l'individu qui passe la frontière. Mais si après un passage avec symétrie, il revient au point de départ en marchant le long de la bande, il retrouvera ce qu'il avait laissé tout inversé comme dans le monde symétrique défini ci-dessus. Ce cas ne définit pas de rupture d'espace au centre : si quelqu'un passe par ce point, il réapparait ausitôt inversé de l'autre côté. On peut aussi voir ce problème en regardant un trajet effectuer tout drit, mais perpendiculaire à la bande (flèches bleus et rouges) : le rond vert est à gauche où à droite suivant où on se place.
Sur le schéma ci contre, les centres se trouve sur le trait d'axe.
Pour tout habitant de ce pays résidant trop loin des points centrals, leur pays parail être un cylindre comme dans le cas précédent. L'histoire d'inversion peut-être pour eux qu'une légende lointaine. Par contre, plus on habite près du centre de symétrie, plus on rencontre de gens qui se font inverser, plus on peut trouver les livres qui sont écrits à l'envers, moins on est géné par l'inversion. Ceux qui habitent à côté de l'axe de symétrie peuvent même choisir en fonction de leur besoin d'être gaucher ou droitier, parfois ils peuvent aussi saoir écrire dans les deux sens. Mais des inversions trop fréquentes peuvent être fatales à des esprits fragiles.




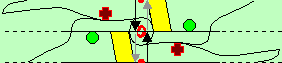
- du même côté, mais avec une symétrie autour d'un point central (comme pour le cas en face, le centre ou poteau de l'autre côté ,est obligatoirement en face). Cette fois, il n'y a plus d'inversion gauche-droite : le centre reste toujours du même côté. Par contre, il y a un problème si quelqu'un veut passer par le centre : il se retrouve face à lui même comme au centre de l'île du monde symétrique. On peut régler ce problème par la présence de gros poteaux comme j'ai aussi fait dans le monde symétrique.
Les flèches grise et noire représentent une trajet en ligne droite (le même trajet pour toutes les copies de l'espace).


Ces mondes, on peut se les représenter autrement. Le premier est en fait un monde cylindrique. Le second on peut se le représenter comme un monde cylindrique avec un bout fermé. Les représentations du troisièmes me semblent moins évidentes. On peut prendre un cylindre avec une particularité : à la frontière on passe de dessus à dessous et vise versa (si vous trouvez mieux, j'attends vos sujections).
Avec de telles représentations on peut peut-être mieux comprendre ces mondes. La représentation cylindrique du premier peut poser des questions quant à la gestion de l'altitude. Imaginez un monde de 1 km de rayon à l'altitude 0. Sa circonférence fait donc 6,283 km. supposons notre bande coupée par un plateau de 1 km d'altitude, à ce niveau, le rayon sera de 2 km, donc le périmètre de 12,566 km. Si notre monde est un monde cylindrique il faut tenir de cette variation du rayon qui implique une variation de la largeur de la bande (moins sensible si le rayon est plus grand, comme pour notre bonne vieille terre).
On peut aussi prendre en compte un dénivelé possible entre les deux bords. Dans ce cas en parcourant nos chemins indiqués par les flèches dans les dessins précédents, soit on monte toujours, soit on descend toujours. Cette particularité pose un problème pour le dernier cas étudier : si sur les flèches de droite on monte, alors sur les flèches de gauche on descend! Cette particularité peut se traduire par une dénivélation assez importante autour des poteaux du centre de symétrie. Quoi qu'il en soit, cette dénivélation présente toujours la possibilité d'avoir une source d'énergie inépuisable : il suffit de faire un canal soit autour des piliers de symétrie dans le dernier cas ou perpendiculaire à la direction principale. Entre deux traversées de plan, on perd la hauteur du dénivelé : on peut mettre une moulin à eau (ou une turbine électrique si la technologie le permet) sur le canal et celui-ci débiterai de l'énergie jusqu'à évaporation de l'eau!
- Les rectangles et autres motifs dallants
Dans ce cas nous n'étudierons que les passages qui donne un déplacement du monde sans le faire pivoter (les translations quoi!). Comme le cas précédant des bandes sans symétrie.
N'oublions pas que les carrés sont des rectangles particuliers : quadrilatères à 3 angles droits (le dernier sera donc automatiquement droit). Si on desside que le motif de répétition sera sur un parallélogramme, ceci revient au même : si on place le motif plusieurs fois, on voit qu'il aurait pu être choisi sur un rectangle ou sur plein d'autres formes pas aussi régulières. Je conseille de choisir soit le rectangle pour la simplicité, soit une forme qui fait bien comprendre les particularités du terrain pour dessiner le motif.
On peut choisir n'importe quel motif qui permet de daller un plan sans changer l'orientation des carreaux si on souhaite pas avoir de points de rupture de l'espace (mes piliers à hauteur
 infinie), on reviendra toujours aux rectangles ou hexagones (aux faces
opposées parallèles).
infinie), on reviendra toujours aux rectangles ou hexagones (aux faces
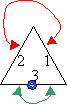
opposées parallèles). 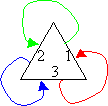 Il existe aussi d'autres motifs
recouvrants comme des triangles, mais si on fait correspondre entre elles deux faces,
que fait-on de la troisième? Une symétrie centrale(dessin de gauche)? Un mur infranchissable?
A moins qu'on desside de faire un monde avec des frontières visibles
et des retours impossibles (dessin de droite). Dans ce cas si on passe
la face 1, on arrive sur la 2 et si on revient sur nos pas, on retourne à la 3! Dans le
cas des triangles, on sort du cas recouvrant car on a une autre transformation plane que la translation.
Il existe aussi d'autres motifs
recouvrants comme des triangles, mais si on fait correspondre entre elles deux faces,
que fait-on de la troisième? Une symétrie centrale(dessin de gauche)? Un mur infranchissable?
A moins qu'on desside de faire un monde avec des frontières visibles
et des retours impossibles (dessin de droite). Dans ce cas si on passe
la face 1, on arrive sur la 2 et si on revient sur nos pas, on retourne à la 3! Dans le
cas des triangles, on sort du cas recouvrant car on a une autre transformation plane que la translation.
- Le cercle
- Les frontières


