Cette page est accompagnée d'un fichier excel :( avec toutes les méthodes de calcul afin de mieux comprendre comment les résultats sont trouvés et d'un fichier scilab :).

Attention, cette page était mon premier centre d'essai JavaScript. En promenant votre souris, vous pouvez avoir de gentilles surprises ! À vous de les trouver.

1. Vocabulaire - Méthodes - Cours

   Aucune démonstration n'est faite ici. Il y a juste quelques notions pour mieux comprendre la suite et faire d'autres probabilités sur des cas pouvant vous intéresser. Pour des joueurs uniquement intéressés par les résultats, voir uniquement le fichier excel associé ou le fichier scilab.

   1. Présentation

      Deux méthodes principales sont proposées.

      La première (utilisée dans les deux premières études) consiste à compter (dénombrer) le nombre de possibilités de chaque événement (possibilité) et à le comparer au nombre total de possibilité. Cette méthode est valable quand les possibilités sont facilement dénombrables.

      La seconde consiste à utiliser les probabilités. La probabilité d'un événement est le rapport du nombre de possibilités de cet événement par le nombre total des possibilités. Cette méthode est utilisée par exemple au quatrième tableau car elle permet grâce à des propriétés énumérées par la suite d'éviter de compter tous les cas.

   2. Vocabulaire

      événement élémentaire : pour le jet d'un dé à 6 faces, les évènements élémentaires sont faire «1», «2», «3», «4», «5» ou «6». Pour un jet de 2 dés, «faire un total de 6 sur 2 dés» n'est pas un événement élémentaire, par contre faire «1 et 5», «2 et 4», «3 et 3», «4 et 2» ainsi que «5 et 1» sont des événements élémentaires (attention il faut prendre en compte l'ordre des dés). L'événement «faire un total de 6» est l'union de tous ces évènements élémentaires.
      univers : l'ensemble des événements élémentaires est appelé univers, comme faire «1», «2», «3», «4», «5» ou «6» avec un dé à 6 faces. Dans cet exemple, on a U={1,2,3,4,5,6}.

      événements incompatibles : ils ne peuvent pas être réalisés simultanément comme faire sur un jet de deux dès au moins un «5» et «avoir une somme de 4».

      événements contraires : A et B sont des événements contraires si B contient tous les événements élémentaires ne se trouvant pas dans A. On note B=A. Par exemple A : «obtenir un résultat pair» et B : «obtenir un résultat impair».

      événement A et B : tous les événements élémentaires se trouvant à la fois dans A et B. Si A est faire un multiple de trois et B faire un nombre pair sur la somme de deux jets de dés, «A et B»= AB= «Faire 6 ou 12»

      événement A ou B : tous les événements se trouvant soit dans A soit dans B. Avec l'exemple précédant ceci donnera «A ou B»= AUB= «Faire 2, 3, 4, 6, 8, 9, 10 ou 12».

      équiprobabilité : on dit qu'on a les conditions d'équiprobabilité quand tous les événements élémentaires ont la même probabilité. Pour des dès non truqués, on a équiprobabilité. Dans ce cas, on a : p(A)=card(A)/card(U) avec card A qui est égal au nombre d'événements élémentaires de A et card U qui est le nombre d'événements élémentaires total

      événements dépendants : a et b sont dépendants si le résultat de b dépend de a par exemple tirons 2 cartes d'un paquet. On ne peut pas tirer deux fois la même carte & le 2^nd tirage dépend du premier.

      événements indépendants : a et b sont indépendants si le résultat de a n'influe pas sur le résultat de b. Par exemple a résultat du premier dé et b résultat du second dé.

   3. Propriétés
      • Une probabilité est un réel positif entre 0 et 1. On note p(A) la probabilité d'un événement A.
      • La somme de toutes des probabilités de tous les événements élémentaires fait 1. Plus généralement : p(A)+p(A)=1.
      • p(AUB)+p(AB)=p(A)+p(B).Donc si A et B sont incompatibles p(A et B)=0, on a p(AUB)=p(A)+p(B).
      • La somme des probabilités d'un ensemble d'événements incompatibles dont l'union forme tout l'univers est 1 : la ligne total de mes tableaux sert de vérification.
      • A et B étant deux événements indépendants p(AB)=p(A)) x p(B). Par exemple sur deux jets de dés A : le premier tombe sur un nombre pair et B le second dé impair. p(AUB)=p(A) x p(B)=3/6x2/6=1/6 (voir aussi l'équiprobabilité).
      
      
2. Méthodes simples
   1. On jette un seul dé : 1D6

      Les 6 résultats de notre dé sont équiprobables (dé non truqué). Avec les faces numérotées de 1 à 6. Ceci donne comme tableau de probabilités (simple, mais il faut commencer par là) :

   2. On jette deux dés : 2D6

      En faisant la somme des deux dés, on peut obtenir un résultat de 2 à 12. On peut trouver le nombre de possibilités de faire un résultat en faisant le compte (dénombrement) des possibilités. Prenons des exemples :

      • Pour 6 : 1+5 ; 2+4; 3+3 ; 4+2 ; 5+1 ;Þ 5 possibilités : le premier peut aller de 1 à 5.
      • Pour 10 : 4+6 ; 5+5; 6+4 ;Þ 3 possibilités : le premier dès peut aller de 4 à 6.

      Un simple dénombrement suffit car toutes ses possibilités sont équiprobables.

      Ce raisonnement revient à faire dans sa tête le tableau ci-dessous où on a les jets les deux dés et le résultat. On dénombre les résultats égaux sur les diagonales.

      Comme cette méthode sera souvent utilisée avec des données plus complexes qui ne pourraient pas entrer dans un tableau, j'ai préféré l'expliquer sur un cas simple.

   3. On jette trois dés : 3D6

      Une méthode simple consiste à utiliser le tableau déjà fait pour dénombrer les possibilités des deux premiers dés auquel on rajoutera le résultat du troisième dés. Le résultat du 3^ème dés étant indépendant des 2 premiers, on peut utiliser la propriété : p(AÈB)=p(A)xp(B) en comptant toutes les solutions pour obtenir un résultat. Pour 5 par exemple : 5=2+3=3+2=4+1 (3 solutions possibles : 2D6 +1D6) donc p(5)=0,028/6+0,056/6+0,083/6=0,167/6=0,028. Pour vérifier, j'ai rajouté la ligne des possibilités.

      
      
   4. On jette trois dés quelconques

      Une autre méthode qui permet de trouver sans calcul préalable les probabilités des résultats de la somme de 3 dès. Pour ceci, il faut se représenter dans l'espace la somme de trois 3 dès (un tableau à 3 dimensions en forme de cube). Nous avons des plans de d'équations cartésiennes x+y+z=constante où la somme de nos trois dés est constante Il suffit de compter les jets qui sont à l'intersection du plan et du cube.

      En partant du point où les trois dès on fait 1 (résultat 3), on suit les arêtes (flèches 1, 2 et 3 du dessin ci contre) en directions du point où les trois dés ont fait le maximum. Chaque fois que nous passons au point suivant, le total a monté de 1. Ce décompte se fait en trois parties :

      1. Jusqu'au premier sommet :

         Nous avons un triangle qui chaque fois s'élargit et devient plus haut. On parcourt les valeurs de 1 à 6 du dessin ci-dessus où le nombre de faces par dès est de six. À la n^ième valeur, on rajoute n possibilités.

      2. Jusqu'au second sommet :

         Tout en s'élargissant, notre triangle se fait rogner les coins : cases 9 à 12. On continue de rajouter n possibilités, mais il faut enlever les 3 coins : des petits triangles comme au 1. qu'il faut enlever trois fois.

      3. Jusqu'au troisième et dernier sommet :

         c'est comme la première partie, mais dans l'autre sens : cases 13 à 18. Cette partie sera remplie à rebours en remplissant la première : pas besoin de se perdre dans des considérations mathématiques.

      Tableau des possibilités avec un dé à 23456789101112131415161718192021222324 faces.
3. Le meilleur résultat d'une série de 6 fois 3D6

   Ca devient de plus en plus dur !

   1. Exemple simple : le meilleur de deux dés 6

      La première ligne de calculs consiste à trouver quelle chance a-t-on de n'avoir aucun dé dont le résultat est supérieur ou égal à 1, 2, 3, 4, 5 ou 6. On trouve ce résultat de la manière suivante pour 4 par exemple : on ne doit obtenir ni de 4 ni de 5 ni de 6 sur aucun des deux dés. Donc ceci fait 3/6 par dés, donc (3/6)² pour le total.

      La seconde ligne représente les événements contraires à la première. On fait donc 1- la première ligne.

      La troisième découle d'une suite logique : si on a au moins un nombre supérieur ou égal à 4 et aucun supérieur ou égal à 5 on en déduit que le plus grand est 4 donc p(max=4)=p(>=4)-p(>=5)=0,75-0,56=0,19. On fait de même pour tous les autres résultats. ;

      Cet exemple simple peut se dénombrer avec un tableau où on met deux entrées comme le 2^nd tableau du II)B). Ceci n'est pas le cas de l'exemple suivant : on doit jeter 6x3=18 dès à 6 faces ce qui fait un total de 6¹⁸ >10¹⁴ solutions (plus de 100 millions de million ou 100 milliers de milliard !).

   2. Le meilleur résultat d'une série de 6 fois 3D6

      On utilise le même raisonnement que précédemment avec les résultats du tableau 3D6.

      On a du rajouter la première ligne de calculs qui donne la probabilité de faire au moins le résultat affiché avec un seul jet.

      La seconde ligne, faire aucun résultat supérieur ou égal à ce nombre avec 6 jets, sera donc (1- première ligne)⁶ . La parenthèse représente la probabilité qu'un jet (seul) ne soit pas supérieur ou égal au résultat. Les 6 jets étant indépendants le résultat a été mis à l'exposant 6 (on peut changer ce nombre dans le fichier excel).

      La dernière est comme le tableau précédent.

4. La somme des trois meilleurs dès parmi 4

   Le plus dur est pour la fin et on y est !
   Le but de la manœuvre est de faire la somme des 4 dés 6 et de soustraire le plus mauvais dé qu'il faudra donc connaître. On va surtout utiliser les probabilités et les propriétés des événements indépendants.

   1. Premier tableau : pour mieux partir

      Ce premier tableau serait en soit inutile s'il n'était pas conçu uniquement pour mieux comprendre les 2^nd et 3^ème tableaux

      Quand on tire un seul dé, son résultat est à la fois le meilleur et le plus mauvais car il est le seul résultat. La probabilité de faire 5 est 1/6. Dans ce cas le plus mauvais dé possible est 5 les autres ayant une probabilité nulle car on a tiré uniquement 5.

   2. Second tableau

      Ce tableau peut se remplir en dénombrant :
      

      si je fais 1 au premier et 1 au second, le résultat est 2 le plus mauvais dé est 1.

      si je fais 1 au premier et 2 au second, le résultat est 3 le plus mauvais dé est 1.

      ...

      si je fais 5 au premier et 4 au second, le résultat est 9 le plus mauvais dé est 4.

      Puis on divise le nombre de possibilités recensées dans chaque cas par le nombre total de possibilités totales.

      Remarques : une case avec un zéro s'explique simplement : on ne peut pas obtenir ce résultat avec un dé ayant la valeur du plus mauvais dé. Comme, par exemple, il est impossible de faire 4 avec un 5 sur un des deux dés ou on ne pas faire 10 si un des deux dés est 1.

      on ne trouve que deux résultats : 0,028 et 0,056 car il n'y a que une ou deux possibilités chaque fois. 0,028 indique que ce résultat est obtenu avec 2 dés identiques comme 8=4+4 (résultat 8 et moins bon dès 4).

   3. troisième tableau

      Ce tableau représente la somme de 4 dès 6 avec comme information, le plus mauvais des 4 dés. Comme 4=2+2, j'ai utilisé le tableau précédent. Le raisonnement est un dénombrement de possibilité :

      • pour faire 4 on dispose de 2+2 : probabilité 0,028 x 0,028 avec 1 et 1 comme plus mauvais dés, on retient 1.
      • ...
      • pour faire 9 on dispose de 2+7 ; 3+6 ; 4+5 ; 5+4 ; 6+3 ; 7+2.
        • pour faire 2+7 on a une probabilité de
          • 0,028 x 0,056 avec 1 et 1 comme plus mauvais dés, on retient 1
          • 0,028 x 0,056 avec 1 et 2 comme plus mauvais dés, on retient 1
          • 0,028 x 0,056 avec 1 et 3 comme plus mauvais dés, on retient 1
        • pour faire 3+6 on a une probabilité de...
        • ...
        • pour faire 7+2...
      • pour faire 10 ...
      • ...
      • pour faire 24 on dispose de 12+12 : probabilité 0,028 x 0,028 avec 6 comme plus mauvais dés, on retient 1.

      Puis on fait la somme de tous ces cas (voir dans le fichier excel procédure VBA quatre_D_six, la procédure deux_D_six fait le même raisonnement pour trouver le tableau précédent)

      Un 0 dans une case indique un événement impossible : on ne peut pas faire 24 avec 1 comme plus mauvais résultat ! Avec un 1 sur un des 3 dès le résultat le plus élevé est 3x6+1=19.

   4. La somme des trois meilleurs dés

      On parcourt le tableau et on soustrait à la somme des 4 dés 6 le plus mauvais. Ceci donnera un résultat et la probabilité de l'obtenir. Un résultat étant obtenu de plusieurs manières, il faut donc additionner les probabilités de chaque possibilité. Par exemple pour 8=9-1=10-2 (11-3 est impossible car si on a 3 comme plus mauvais dé le résultat vaut au moins 12=4x3). La probabilité sera de 0,04+0,008=0,048.

      Ceci est aussi traité par une procédure VBA.

   5. Même calcul en fonction du plus mauvais dé

      Cette fois, on va raisonner en fonction du plus mauvais dé : le nombre de possibilité de ce qui reste faisable.

      • Si le plus mauvais dé n'apparaît qu'une fois (pas compté dans les trois meilleurs). On fait comme si sur le dé il n'y a que des nombres supérieurs strictement au plus petit. Les résultats sont donc ceux du #II.D avec un dé à 5, 4, 3, 2, 1 face(s) auxquels on rajoute respectivement 3, 6, 9, 12 et 15 :

        Le plus mauvais pouvant être en 4= positions différentes, ce résultat est à multiplier par 4

      • Si le plus mauvais apparaît 2 fois (compté une fois dans les trois meilleurs) :

        Cette fois, nous avons 6= façons de placer ces 2 sur les 4 places disponibles. Il faudra donc multiplier par 6 le résultat précédent.

      • Si le plus mauvais dé apparaît 3 fois (compté deux fois dans les trois meilleurs) :

        Le plus mauvais pouvant être en 4= positions différentes, ce résultat est à multiplier par 4.

      • Si le plus mauvais dé apparaît 4 fois (compté trois fois dans les trois meilleurs) :

        Le plus mauvais pouvant être en 1= positions différentes, ce résultat est à multiplier par 1.

      • Le résultat final est donc :
5. Bilan récapitulatif des trois possibilités

   

6. Les trois meilleurs parmi n>=4 tirages

   On reprend l'étude précédente et on commence par discuter sur les dés non comptés. Ces dès sont inférieurs où égal au plus mauvais des 4 meilleurs qui vaut m pour notre calcul.

   Combien de places peuvent-ils occuper ? Il faut prendre en compte, comme tout à l'heure une redondance de m parmi les dès comptés. On reprend donc les 4 tableaux de dénombrement.

   • Le premier : m pas compté dans les trois meilleurs

     Il faut donc placer n-3 trous parmi n places : ==n(n-1)(n-2)/6.

     • Combien de possibilités pour remplir ces trous ?

       On a donc n-3 dés plus petits ou égaux à m, donc m^(n-3) possibilités, mais il est impossible que tous soient plus petit que m (plus petit ou égal à m-1) : (m-1)^(n-3) possibilités. On a donc chaque fois m^(n-3)-(m-1)^(n-3) possibilités pour les dés non comptés.

   • Le second : m compté une fois dans les trois meilleurs

     Il faut donc placer n-2 trous parmi n places : ==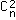n(n-1)/2.

     • Combien de possibilités pour remplir ces trous ?

       On a donc n-2 dés plus petits ou égaux à m, donc m^(n-2) possibilités, mais il est impossible que tous soient plus petit que m : (m-1)^(n-2) possibilités et il est aussi impossible que tous sauf 1 soient inférieurs à m : (m-1)^(n-3) (dans ce cas, on aurait un m dans les n-2 trous, on peut lui trouver =n-2 places différentes). On a donc chaque fois m^(n-2)-(m-1)^(n-2)-(m-1)^(n-3)(n-2) possibilités pour les dés non comptés.

   • Le troisième : m compté deux fois dans les trois meilleurs

     Il faut donc placer n-1 trous parmi n places : ==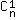n.

     • Combien de possibilités pour remplir ces trous ?

       On a donc n-1 dés plus petits ou égaux à m, donc m^(n-1) possibilités, mais il est impossible que tous soient plus petit que m : (m-1)^(n-1) possibilités, il est aussi impossible que tous sauf 1 soient inférieurs à m : (m-1)^(n-2) dans ce cas, on aurait un m dans les n-1 trous, on peut lui trouver 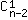=n-1 places différentes) et il est aussi impossible que tous sauf 2 soient inférieurs à m : (m-1)^(n-3) (dans ce cas, on aurait deux m dans les n-1 trous, on peut leur trouver =(n-1)(n-2)/2 places différentes). On a donc chaque fois m^(n-1)-(m-1)^(n-1)-(m-1)^(n-2)(n-1)-(m-1)^(n-3)(n-1)(n-2)/2 possibilités pour les dés non comptés.

   • Le quatrième : m compté trois fois dans les trois meilleurs

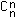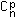     Les 4 meilleurs dés ont donné m, les autres au plus m : "n trous parmi n places" donne ==1 possibilité

     • Combien de possibilités pour remplir ces trous ?

       On a donc n dés plus petits ou égaux à m, donc mⁿ possibilités, mais il est impossible que tous soient plus petit que m : (m-1)ⁿ possibilités, il est aussi impossible que tous sauf 1 soient inférieurs à m : (m-1)^(n-1) dans ce cas, on aurait un m dans les n trous, on peut lui trouver 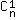=n places différentes) et il est aussi impossible que tous sauf 2 soient inférieurs à m : (m-1)^(n-2) (dans ce cas, on aurait deux m dans les n trous, on peut leur trouver 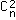=n(n-1)/2 places différentes), il est aussi impossible que tous sauf 3 soient inférieurs à m : (m-1)^(n-3) (dans ce cas, on aurait trois m dans les n trous, on peut leur trouver =n(n-1)(n-2)/6 places différentes). On a donc chaque fois mⁿ-(m-1)ⁿ-(m-1)^(n-1)n-(m-1)^(n-2)n(n-1)/2-(m-1)^(n-3)n(n-1)(n-2)/6 possibilités pour les dés non comptés.

   Après ceci, la phase de calculs commence. Pour chaque case de chaque tableau, on doit multiplier le chiffre qui y apparaît par les deux nombres précédement calculés : les possibilités de trous et les possibilités de remplir les trous.

   Tableau des possibilités avec 456789101112131415161718192021222324 tirages.
7. Tirage "dés de moyenne"

   On jette 3 dés du type désiré, et on ne prend en compte que celui du milieu.
   Par exemple, un guerrier qui monte de niveau lance 3D10, et obtient 3, 5 et 8. Se débarrassant des deux résultats les plus hauts et plus bas, son score de dé de vie est de 5.
   Autre exemple, un prêtre lance 3d8, obtient 4, 6 et 6, en ne gardant que le dé du milieu, ça donne 6.

   Tableau avec un dé à 456789101112131415161718192021222324 faces.