
Suites et Banques
Une suite géométrique est une suite qui est de la forme suivante : an+1=r.an. Ceci donne an=rna0. Cette formule permet de calculer rapidement an quand on connaît n, r et a0.
Il existe aussi les suites arithmétiques qui sont simples à exprimer : an+1=an+q. Ceci donne an=a0+nq. Cette formule permet aussi de retrouver facilement an.
Malheureusement, toutes les suites ne sont pas si simple. Parfois, on essaie de retomber sur une telle suite par une transformation simple pour trouver une formule qui donne tous les termes de la suite :par exemple celle qui donne le Rn dans l'étude suivante.
Sur un compte le solde de départ est S0 (réel quelconque). Chaque mois, on verse une mensualité de M (négative si c'est la banque qui nous verse de l'argent), les taux d'intérêts mensuels sont de r-1 (attention, ce n'est pas un % !) ou 100(r-1) % (si r vaux 1.02, le taux sera de 0,02 ou 2%).
Ceci donne avec Sn la somme disponible au nième mois : Sn=rSn-1+M. Cette suite n'est ni géométrique, ni algébrique. On va la modifier afin qu'elle devienne géométrique : Rn=Sn+C ou Sn=Rn-C avec C constante choisie spécialement pour que Rn soit géométrique. Rn est un intermédiaire de calcul qui ne représente rien ! Tout comme C.
Cela implique : Rn-C=r(Rn-1-C)+M d'où Rn=rRn-1-rC+M+C. Pour que ceci soit une suite géométrique, il faut que la constante -rC+M+C soit nulle. Ça nous impose C=M/(r-1).
Rn étant une suite géométrique, on a donc Rn=rnR0=rn(S0+C), donc Sn=rn(S0+C)-C
Comparer un premier placement de 100 Euros à 100% sur 10 ans (vu en publicité) et un second de 100 Euros à 8% par an qu'on laisse 10 ans.
Au bout de 10 ans on aura par le second 100x1,0810 les intérêts arrivent 10 fois en 10 ans : au bout de 1 an on a 100+100*8/100=100x1,08=108 Euros, de 2 ans 108+108x8/100=108x1,08... Ceci donne à la fin pour le second 215,89 Euros =100x1,0810 alors que pour le premier on aurait que 200 Euros.
En conclusion l'intérêt annuel d'un placement à 100% sur 10 ans n'est pas 100%/10=10% car il est inférieur à 8% ! En fait chaque année on multiplie par la racine dixième de (1+100/100)=2 qui vaut 1,0718. Donc 100% sur 10 ans équivaut à 7,18% par an.
Finalement : méfiez-vous des publicités (pour les placements). Réfléchissez bien avant de trouver le meilleur. Les publicités sont faites pour tromper.
Sur un an il y a 12 mois, donc un taux de ta% annuel donne tm% par mois. tm vérifie (1+tm/100)12=1+ta/100.
Ceci donne ta=100(1+tm/100)12-100 et 1+tm/100 est la racine 12ème de 1+ta/100.
Voici la formule : 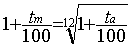
Exemple : 6% par an donne 0,487% par mois. Chaque mois le montant est multiplié par 1,00487 et 1,0048712=1,060031 donc au bout de 1 an on a bien un gain de 6%.
Attention : si les virements ou rentes sont mensuels, il faut prendre les intérêts mensuels alors qu'on parle toujours en intérêts annuels.
Exemple : soit un placement à 12% par an. On pourrait dire trop rapidement que ça représente 1% par mois!
À 1% par mois, ceci donne :
1er mois : 100x1,01=101
2eme mois : 101x1,01=102,01
3eme mois : 102,01x1,01=103,0301
4eme mois : 103,0301x1,01=104,0604
5eme mois : 104,0604x1,01=105,1010
6eme mois : 105,1010x1,01=106,1520
7eme mois : 106,1420x1,01=107,2135
8eme mois : 107,2135x1,01=108,2856
9eme mois : 108,2856x1,01=109,3684
10eme mois : 109,3684x1,01=110,4520
11eme mois : 110,4520x1,01=111,5565
12eme mois : 111,5565x1,01=112,6720
Ceci fait finalement un placement à 12,67%!!
Écrivez votre taux dans la case et vous aurez la convertion taux mensuel en taux annuel ainsi que la convertion taux annuel => taux mensuel en cliquant sur OK.
Ce cas correspond à S0<0 et M>0.
Le remboursement est fini quand Sn=0, donc quand rn(S0+C)=C ou
rn(S0+ M/(r-1))= M/(r-1), rn(S0(r-1)+M)=M.
Dans cette relation, on a un intérêt mensuel de 100(r-1)%, n nombre de mois, S0 montant de l'emprunt et M mensualité.
En résolvant l'équation, on trouve : M=S0(r-1)rn/(1-rn).
On peut vérifier que si n=1 on a bien M=-rS0 (une vérification n'est jamais superflue).
Application numérique : r=1,0056 S0=15000, n=60 ou n=120 (5ans ou 10 ans) donc M=295 Euros/mois ou M=172 Euros/mois.
On a emprunté 15000 et remboursé 17700 Euros ou 20640Euros.
La première étape consiste à isoler le rn : rn=M/(S0(r-1)+M).
Grâce au logarithme, l'exposant passe en facteur : nln(r)=ln(M/(S0(r-1)+M)) donc n= ln( M/(S0(r-1)+M))/ln(r)
A.N. : r=1 ,0056, S0=15000 Euros et M=600 Euros donnent : n=58,8 mois (c'est normal que le
compte ne soit pas juste). On peut rembourser sur 58 mois en remboursant un peu
plus chaque mois ou sur 59 mois en remboursant un peu moins chaque mois. On peut aussi payer 600 Euros par mois pendant 58 mois et un peu moins
le dernier (voir tableau d'amortissement).
Il faut faire des essais : la durée (M fixe) ou le montant (n fixe) est une fonction croissante de r, il faut donc trouver une valeur supérieure et une autre inférieure. Puis on resserre l'encadrement jusqu'à la précision recherchée (résolution par dichotomie).
Attention aux arnaques : les banques parlent aussi en TEG pour donner les taux. Un taux à 5,35% TEG est pratiquement un taux véritable de 5,5% (comme l'emprunt pour ma maison en 1998 !). Pour le calcul exact du coût il faut aussi prendre en compte l'assurance du prêt.
Une variation (remboursement moins élevé) est toujours (ou presque) présente le dernier mois car il est normal que les calculs ne tombent pas justes.
Ce tableau peut être utile quand on fait un remboursement (partiel ou total) ou quand on change les mensualités :
il permet de savoir où on en est afin de recommencer les calculs sur de nouvelles bases.
Attention : Le second tableau s'affiche en bas du premier.
Exemple : On place pendant 10 ans 100 Euros par mois sur un compte bloqué à 4,5% (par an).
Ceci fait 0,36748% par mois, donc
Sn=C(1,0036748120-1)=15047,56 avec C=100/0,0036748=27212.30. On a 15047,56 Euros alors qu'on a placé 12000 Euros.
Même méthode qu'au II), mais on n'a plus « =0 » mais « =Sn ».
Exemple : on a 10000 Euros à placer, on dépose 100 Euros de plus par mois à 4,5%, le but étant d'avoir 20000 Euros. Combien de mois doit-on attendre. Le taux est le même que précédemment, la constante C aussi.
La formule donne rn=(20000+C)/(10000+C)=1,2687. n=ln(1,2687)/ln(1,0036748)=64,88. Les 20000 Euros seront atteints (et dépassés) en 65 mois, ou 5 ans et 5 mois.
Ici on place une certaine somme, et tous les mois, on en récupère une partie. Si la somme qu'on retire est inférieure aux intérêts alors la somme placée augmentera petit à petit. Si on choisi une rente égale aux intérêts alors le montant placé restera inchangé. Par contre si on récupère chaque mois plus d'argent que les intérêts alors la somme ira en diminuant jusquà attendre le total fatidique de 0.
La résolution se fait comme le reste, il faut juste voir dans quel cas on se place.
Exemple : J'ai 1 000 000 € à placer. Je trouve un placement à 6% et je veux 5000 € par mois. 6% par an donne 0,4867% par mois, par mois, au départ, je gagne 4867 Euros : mon placement va diminuer au cours des ans. Je veux donc savoir combien de temps je vais pouvoir avoir 5000 Euros par mois, je cherche donc Sn=0.
rn=M/(S0(r-1)+M)=37,75. n=ln(37,75)/ln(1,004867)=747,77 mois donc plus de 62 ans! Le temps serai infini si on avait choisi une rente inférieure ou égale à 4867 Euros.
Avant de réver, penser à l'inflation qui diminue la valeur réelle de la rente dans le temps ainsi que la valeur placée.
Pour toute question supplémentaire : troumad@libertysurf.fr